Come risolvere i problemi con la parabola?

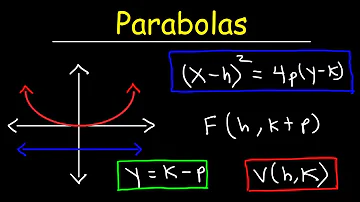
Come risolvere i problemi con la parabola?

6:2313:56Clip suggerito · 60 secondiParabola Esercizi Svolti - YouTubeYouTubeInizio del clip suggeritoFine del clip suggerito

Quali sono le caratteristiche di una parabola?

La parabola è il luogo geometrico dei punti del piano equidistanti da un punto fisso detto fuoco e da una retta detta direttrice; in termini più generali una parabola è una conica non degenere. ... In questo frangente porremo particolare attenzione alle formule per il calcolo di vertice, asse, fuoco e direttrice.

Come risolvere l'equazione della parabola?

y = ax2 + bx + c. Abbiamo così ottenuto l'EQUAZIONE DELLA PARABOLA.

Quando la parabola è rivolta verso il basso?

In particolare, se a > 0 a > 0 a>0 la parabola è rivolta verso l'alto, mentre se a < 0 a < 0 a

Come trovare l'equazione di una parabola dati 3 punti?

EQUAZIONE DELLA PARABOLA PASSANTE PER TRE PUNTI

1. y = ax2 + bx + c. Se un punto appartiene ad una parabola, le sue coordinate ne verificano l'equazione: quindi, la parabola passante per Asarà: 3 = a(1)2 + b(1) + c.
2. 3 = a + b + c. La parabola passante per B sarà: 2 = a(2)2 + b(2) + c.
3. 2 = 4a + 2b + c. advertising.

Come si determinano le caratteristiche di una parabola nota l'equazione?

I coefficienti dell'equazione della parabola in forma esplicita y = ax2 + bx + c danno immediate informazioni sulla forma e sulla posizione della curva nel piano cartesiano.

How do you solve a parabola?

• How to Solve a Parabola. The quadratic function is ax^2+bx+c = 0, where a, b, and c are numbers called coefficients. The solution for any quadratic equation or parabola can be found by using a little algebra and the general formula for the quadratic equation, which is : x = -b ± sqrt (b^2 - 4ac) / 2a.

What are the key features of a parabola?

• The key features of a parabola are its vertex, axis of symmetry, focus, directrix, and latus rectum. See [link]. When given a standard equation for a parabola centered at the origin, we can easily identify the key features to graph the parabola.

How to solve a parabola?

• Using the vertex form of a parabola f (x) = a (x - h) 2+k where (h,k) is the vertex of the parabola.
• The axis of symmetry is x = 0 so h also equals 0.
• a = 1.
• Substituting the a value into the first equation of the linear system:
• k = 3.
• f (1) = 4 = (1 - 0) 2+3 = 1+3.
• f (2) = 7 = (2 - 0) 2+3 = 4+3.

What is the function of a parabola?

• Technically, a parabola is a curve, a function is a mapping, so one is a geometric object and the other is an algebraic object. However, if you don’t want to be too technical, you can think of both as sets of ordered pairs of real numbers.